Differential Equations - Systems: Complex Eigenvalues

In this section we will look at solutions to

$${\overrightarrow{x}}^{\prime }=A\overrightarrow{x}$$

where the eigenvalues of the matrix $A$ are complex. With complex eigenvalues we are going to have the same problem that we had back when we were looking at second order differential equations. We want our solutions to only have real numbers in them, however since our solutions to systems are of the form,

$$\overrightarrow{x}=\overrightarrow{\eta }{e}^{\lambda t}$$

we are going to have complex numbers come into our solution from both the eigenvalue and the eigenvector. Getting rid of the complex numbers here will be similar to how we did it back in the second order differential equation case but will involve a little more work this time around. It’s easiest to see how to do this in an example.

Example 1 Solve the following IVP.$${\overrightarrow{x}}^{\prime }=\left(\begin{array}{cc}3& 9\\ -4& -3\end{array}\right)\overrightarrow{x}\overrightarrow{x}\left(0\right)=\left(\begin{array}{c}2\\ -4\end{array}\right)$$

We first need the eigenvalues and eigenvectors for the matrix.
$$\begin{array}{cc}det\left(A-\lambda I\right)& =\left|\begin{array}{cc}3-\lambda & 9\\ -4& -3-\lambda \end{array}\right|\\ & ={\lambda }^2+27{\lambda }_{1,2}=\pm 3\sqrt{3}i\end{array}$$So, now that we have the eigenvalues recall that we only need to get the eigenvector for one of the eigenvalues since we can get the second eigenvector for free from the first eigenvector.
${\lambda }_1=3\sqrt{3}i$:
We need to solve the following system.
$$\left(\begin{array}{cc}3-3\sqrt{3}i& 9\\ -4& -3-3\sqrt{3}i\end{array}\right)\left(\begin{array}{c}{\eta }_1\\ {\eta }_2\end{array}\right)=\left(\begin{array}{c}0\\ 0\end{array}\right)$$Using the first equation we get,
$$\begin{array}{cc}\left(3-3\sqrt{3}i\right){\eta }_1+9{\eta }_2& =0\\ {\eta }_2& =-\frac{1}{3}\left(1-\sqrt{3}i\right){\eta }_1\end{array}$$So, the first eigenvector is,
$$\begin{array}{cc}\overrightarrow{\eta }& =\left(\begin{array}{c}{\eta }_1\\ -\frac{1}{3}\left(1-\sqrt{3}i\right){\eta }_1\end{array}\right)\\ {\overrightarrow{\eta }}^{\left(1\right)}& =\left(\begin{array}{c}3\\ -1+\sqrt{3}i\end{array}\right){\eta }_1=3\end{array}$$When finding the eigenvectors in these cases make sure that the complex number appears in the numerator of any fractions since we’ll need it in the numerator later on. Also try to clear out any fractions by appropriately picking the constant. This will make our life easier down the road.
Now, the second eigenvector is,
$${\overrightarrow{\eta }}^{\left(2\right)}=\left(\begin{array}{c}3\\ -1-\sqrt{3}i\end{array}\right)$$However, as we will see we won’t need this eigenvector.
The solution that we get from the first eigenvalue and eigenvector is,
$${\overrightarrow{x}}_1\left(t\right)=e^{3\sqrt{3}it}\left(\begin{array}{c}3\\ -1+\sqrt{3}i\end{array}\right)$$So, as we can see there are complex numbers in both the exponential and vector that we will need to get rid of in order to use this as a solution. Recall from the complex roots section of the second order differential equation chapter that we can use Euler’s formula to get the complex number out of the exponential. Doing this gives us,
$${\overrightarrow{x}}_1\left(t\right)=\left(\cos \left(3\sqrt{3}t\right)+i\sin \left(3\sqrt{3}t\right)\right)\left(\begin{array}{c}3\\ -1+\sqrt{3}i\end{array}\right)$$The next step is to multiply the cosines and sines into the vector.
$${\overrightarrow{x}}_1\left(t\right)=\left(\begin{array}{c}3\cos \left(3\sqrt{3}t\right)+3i\sin \left(3\sqrt{3}t\right)\\ -\cos \left(3\sqrt{3}t\right)-i\sin \left(3\sqrt{3}t\right)+\sqrt{3}i\cos \left(3\sqrt{3}t\right)-\sqrt{3}\sin \left(3\sqrt{3}t\right)\end{array}\right)$$Now combine the terms with an “$i$” in them and split these terms off from those terms that don’t contain an “$i$”. Also factor the “$i$” out of this vector.
$$\begin{array}{cc}{\overrightarrow{x}}_1\left(t\right)& =\left(\begin{array}{c}3\cos \left(3\sqrt{3}t\right)\\ -\cos \left(3\sqrt{3}t\right)-\sqrt{3}\sin \left(3\sqrt{3}t\right)\end{array}\right)+i\left(\begin{array}{c}3\sin \left(3\sqrt{3}t\right)\\ -\sin \left(3\sqrt{3}t\right)+\sqrt{3}\cos \left(3\sqrt{3}t\right)\end{array}\right)\\ & =\overrightarrow{u}\left(t\right)+i\overrightarrow{v}\left(t\right)\end{array}$$Now, it can be shown (we’ll leave the details to you) that $\overrightarrow{u}\left(t\right)$ and $\overrightarrow{v}\left(t\right)$ are two linearly independent solutions to the system of differential equations. This means that we can use them to form a general solution and they are both real solutions.
So, the general solution to a system with complex roots is
$$\overrightarrow{x}\left(t\right)=c_1\overrightarrow{u}\left(t\right)+c_2\overrightarrow{v}\left(t\right)$$where $\overrightarrow{u}\left(t\right)$ and $\overrightarrow{v}\left(t\right)$ are found by writing the first solution as
$$\overrightarrow{x}\left(t\right)=\overrightarrow{u}\left(t\right)+i\overrightarrow{v}\left(t\right)$$For our system then, the general solution is,
$$\overrightarrow{x}\left(t\right)=c_1\left(\begin{array}{c}3\cos \left(3\sqrt{3}t\right)\\ -\cos \left(3\sqrt{3}t\right)-\sqrt{3}\sin \left(3\sqrt{3}t\right)\end{array}\right)+c_2\left(\begin{array}{c}3\sin \left(3\sqrt{3}t\right)\\ -\sin \left(3\sqrt{3}t\right)+\sqrt{3}\cos \left(3\sqrt{3}t\right)\end{array}\right)$$We now need to apply the initial condition to this to find the constants.
$$\left(\begin{array}{c}2\\ -4\end{array}\right)=\overrightarrow{x}\left(0\right)=c_1\left(\begin{array}{c}3\\ -1\end{array}\right)+c_2\left(\begin{array}{c}0\\ \sqrt{3}\end{array}\right)$$This leads to the following system of equations to be solved,
$$\begin{array}{c}3c_1=2\\ -c_1+\sqrt{3}{c}_2=-4\end{array}\}\Rightarrow c_1=\frac{2}{3},c_2=\frac{-10}{3\sqrt{3}}$$The actual solution is then,
$$\overrightarrow{x}\left(t\right)=\frac{2}{3}\left(\begin{array}{c}3\cos \left(3\sqrt{3}t\right)\\ -\cos \left(3\sqrt{3}t\right)-\sqrt{3}\sin \left(3\sqrt{3}t\right)\end{array}\right)-\frac{10}{3\sqrt{3}}\left(\begin{array}{c}3\sin \left(3\sqrt{3}t\right)\\ -\sin \left(3\sqrt{3}t\right)+\sqrt{3}\cos \left(3\sqrt{3}t\right)\end{array}\right)$$

As we did in the last section we’ll do the phase portraits separately from the solution of the system in case phase portraits haven’t been taught in your class.

Example 2 Sketch the phase portrait for the system.$${\overrightarrow{x}}^{\prime }=\left(\begin{array}{cc}3& 9\\ -4& -3\end{array}\right)\overrightarrow{x}$$

When the eigenvalues of a matrix $A$ are purely complex, as they are in this case, the trajectories of the solutions will be circles or ellipses that are centered at the origin. The only thing that we really need to concern ourselves with here are whether they are rotating in a clockwise or counterclockwise direction.
This is easy enough to do. Recall when we first looked at these phase portraits a couple of sections ago that if we pick a value of $\overrightarrow{x}\left(t\right)$ and plug it into our system we will get a vector that will be tangent to the trajectory at that point and pointing in the direction that the trajectory is traveling. So, let’s pick the following point and see what we get.
$$\overrightarrow{x}=\left(\begin{array}{c}1\\ 0\end{array}\right)\Rightarrow {\overrightarrow{x}}^{\prime }=\left(\begin{array}{cc}3& 9\\ -4& -3\end{array}\right)\left(\begin{array}{c}1\\ 0\end{array}\right)=\left(\begin{array}{c}3\\ -4\end{array}\right)$$Therefore, at the point $\left(1,0\right)$ in the phase plane the trajectory will be pointing in a downwards direction. The only way that this can be is if the trajectories are traveling in a clockwise direction.
Here is the sketch of some of the trajectories for this problem.

The equilibrium solution in the case is called a center and is stable.

Note in this last example that the equilibrium solution is stable and not asymptotically stable. Asymptotically stable refers to the fact that the trajectories are moving in toward the equilibrium solution as $t$ increases. In this example the trajectories are simply revolving around the equilibrium solution and not moving in towards it. The trajectories are also not moving away from the equilibrium solution and so they aren’t unstable. Therefore, we call the equilibrium solution stable.

Not all complex eigenvalues will result in centers so let’s take a look at an example where we get something different.

Example 3 Solve the following IVP.$${\overrightarrow{x}}^{\prime }=\left(\begin{array}{cc}3& -13\\ 5& 1\end{array}\right)\overrightarrow{x}\overrightarrow{x}\left(0\right)=\left(\begin{array}{c}3\\ -10\end{array}\right)$$

Let’s get the eigenvalues and eigenvectors for the matrix.
$$\begin{array}{cc}det\left(A-\lambda I\right)& =\left|\begin{array}{cc}3-\lambda & -13\\ 5& 1-\lambda \end{array}\right|\\ & ={\lambda }^2-4\lambda +68{\lambda }_{1,2}=2\pm 8i\end{array}$$Now get the eigenvector for the first eigenvalue.
${\lambda }_1=2+8i$:
We need to solve the following system.
$$\left(\begin{array}{cc}1-8i& -13\\ 5& -1-8i\end{array}\right)\left(\begin{array}{c}{\eta }_1\\ {\eta }_2\end{array}\right)=\left(\begin{array}{c}0\\ 0\end{array}\right)$$Using the second equation we get,
$$\begin{array}{cc}5{\eta }_1+\left(-1-8i\right){\eta }_2& =0\\ {\eta }_1& =\frac{1}{5}\left(1+8i\right){\eta }_2\end{array}$$So, the first eigenvector is,
$$\begin{array}{cc}\overrightarrow{\eta }& =\left(\begin{array}{c}\frac{1}{5}\left(1+8i\right){\eta }_2\\ {\eta }_2\end{array}\right)\\ {\overrightarrow{\eta }}^{\left(1\right)}& =\left(\begin{array}{c}1+8i\\ 5\end{array}\right){\eta }_2=5\end{array}$$The solution corresponding to this eigenvalue and eigenvector is
$$\begin{array}{cc}{\overrightarrow{x}}_1\left(t\right)& =e^{\left(2+8i\right)t}\left(\begin{array}{c}1+8i\\ 5\end{array}\right)\\ & =e^{2t}{e}^{8it}\left(\begin{array}{c}1+8i\\ 5\end{array}\right)\\ & =e^{2t}\left(\cos \left(8t\right)+i\sin \left(8t\right)\right)\left(\begin{array}{c}1+8i\\ 5\end{array}\right)\end{array}$$As with the first example multiply cosines and sines into the vector and split it up. Don’t forget about the exponential that is in the solution this time.
$$\begin{array}{cc}{\overrightarrow{x}}_1\left(t\right)& =e^{2t}\left(\begin{array}{c}\cos \left(8t\right)-8\sin \left(8t\right)\\ 5\cos \left(8t\right)\end{array}\right)+i{e}^{2t}\left(\begin{array}{c}8\cos \left(8t\right)+\sin \left(8t\right)\\ 5\sin \left(8t\right)\end{array}\right)\\ & =\overrightarrow{u}\left(t\right)+i\overrightarrow{v}\left(t\right)\end{array}$$The general solution to this system then,
$$\overrightarrow{x}\left(t\right)=c_1{e}^{2t}\left(\begin{array}{c}\cos \left(8t\right)-8\sin \left(8t\right)\\ 5\cos \left(8t\right)\end{array}\right)+c_2{e}^{2t}\left(\begin{array}{c}8\cos \left(8t\right)+\sin \left(8t\right)\\ 5\sin \left(8t\right)\end{array}\right)$$Now apply the initial condition and find the constants.
$$\left(\begin{array}{c}3\\ -10\end{array}\right)=\overrightarrow{x}\left(0\right)=c_1\left(\begin{array}{c}1\\ 5\end{array}\right)+c_2\left(\begin{array}{c}8\\ 0\end{array}\right)$$$$\begin{array}{c}{c}_1+8c_2=3\\ 5c_1=-10\end{array}\}\Rightarrow c_1=-2,c_2=\frac{5}{8}$$The actual solution is then,
$$\overrightarrow{x}\left(t\right)=-2e^{2t}\left(\begin{array}{c}\cos \left(8t\right)-8\sin \left(8t\right)\\ 5\cos \left(8t\right)\end{array}\right)+\frac{5}{8}{e}^{2t}\left(\begin{array}{c}8\cos \left(8t\right)+\sin \left(8t\right)\\ 5\sin \left(8t\right)\end{array}\right)$$

Let’s take a look at the phase portrait for this problem.

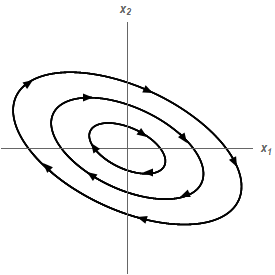
Example 4 Sketch the phase portrait for the system.
$${\overrightarrow{x}}^{\prime }=\left(\begin{array}{cc}3& -13\\ 5& 1\end{array}\right)\overrightarrow{x}$$

When the eigenvalues of a system are complex with a real part the trajectories will spiral into or out of the origin. We can determine which one it will be by looking at the real portion. Since the real portion will end up being the exponent of an exponential function (as we saw in the solution to this system) if the real part is positive the solution will grow very large as $t$ increases. Likewise, if the real part is negative the solution will die out as $t$ increases.
So, if the real part is positive the trajectories will spiral out from the origin and if the real part is negative they will spiral into the origin. We determine the direction of rotation (clockwise vs. counterclockwise) in the same way that we did for the center.
In our case the trajectories will spiral out from the origin since the real part is positive and
$${\overrightarrow{x}}^{\prime }=\left(\begin{array}{cc}3& -13\\ 5& 1\end{array}\right)\left(\begin{array}{c}1\\ 0\end{array}\right)=\left(\begin{array}{c}3\\ 5\end{array}\right)$$will rotate in the counterclockwise direction as the last example did.
Here is a sketch of some of the trajectories for this system.

Here we call the equilibrium solution a spiral (oddly enough…) and in this case it’s unstable since the trajectories move away from the origin.

If the real part of the eigenvalue is negative the trajectories will spiral into the origin and in this case the equilibrium solution will be asymptotically stable.