In this section we need to take a look at the equation of a line in R 3 R 3 . As we saw in the previous section the equation y = m x + b y = m x + b does not describe a line in R 3 R 3 , instead it describes a plane. This doesn’t mean however that we can’t write down an equation for a line in 3-D space. We’re just going to need a new way of writing down the equation of a curve. So, before we get into the equations of lines we first need to briefly look at vector functions. We’re going to take a more in depth look at vector functions later. At this point all that we need to worry about is notational issues and how they can be used to give the equation of a curve. The best way to get an idea of what a vector function is and what its graph looks like is to look at an example. So, consider the following vector function. → r ( t ) = ⟨ t , 1 ⟩ r → ( t ) = ⟨ t , 1 ⟩ A vector function is a function that takes one or more variables, one in this case, and returns a...
Separable Equations
We are now going to start looking at nonlinear first order differential equations. The first type of nonlinear first order differential equations that we will look at is separable differential equations.
A separable differential equation is any differential equation that we can write in the following form.
Note that in order for a differential equation to be separable all the 's in the differential equation must be multiplied by the derivative and all the 's in the differential equation must be on the other side of the equal sign.
To solve this differential equation we first integrate both sides with respect to to get,
Now, remember that is really and so we can use the following substitution,
Applying this substitution to the integral we get,
At this point we can (hopefully) integrate both sides and then back substitute for the on the left side. Note, that as implied in the previous sentence, it might not actually be possible to evaluate one or both of the integrals at this point. If that is the case, then there won’t be a lot we can do to proceed using this method to solve the differential equation.
Now, the process above is the mathematically correct way of doing solving this differential equation. Note however, that if we “separate” the derivative as well we can write the differential equation as,
We obviously can’t separate the derivative like that, but let’s pretend we can for a bit and we’ll see that we arrive at the answer with less work.
Now we integrate both sides of this to get,
So, if we compare and we can see that the only difference is on the left side and even then the only real difference is has the integral in terms of and has the integral in terms of . Outside of that there is no real difference. The integral on the left is exactly the same integral in each equation. The only difference is the letter used in the integral. If we integrate and then back substitute in for we would arrive at the same thing as if we’d just integrated from the start.
Therefore, to make the work go a little easier, we’ll just use to find the solution to the differential equation. Also, after doing the integrations, we will have an implicit solution that we can hopefully solve for the explicit solution, . Note that it won't always be possible to solve for an explicit solution.
Recall from the Definitions section that an implicit solution is a solution that is not in the form while an explicit solution has been written in that form.
We will also have to worry about the interval of validity for many of these solutions. Recall that the interval of validity was the range of the independent variable, in this case, on which the solution is valid. In other words, we need to avoid division by zero, complex numbers, logarithms of negative numbers or zero, etc. Most of the solutions that we will get from separable differential equations will not be valid for all values of .
Let’s start things off with a fairly simple example so we can see the process without getting lost in details of the other issues that often arise with these problems.
Example 1 Solve the following differential equation and determine the interval of validity for the solution.
It is clear, hopefully, that this differential equation is separable. So, let’s separate the differential equation and integrate both sides. As with the linear first order officially we will pick up a constant of integration on both sides from the integrals on each side of the equal sign. The two can be moved to the same side and absorbed into each other. We will use the convention that puts the single constant on the side with the ’s given that we will eventually be solving for and so the constant would end up on that side anyway.
So, we now have an implicit solution. This solution is easy enough to get an explicit solution, however before getting that it is usually easier to find the value of the constant at this point. So apply the initial condition and find the value of .
Plug this into the general solution and then solve to get an explicit solution.
Now, as far as solutions go we’ve got the solution. We do need to start worrying about intervals of validity however.
Recall that there are two conditions that define an interval of validity. First, it must be a continuous interval with no breaks or holes in it. Second it must contain the value of the independent variable in the initial condition, x = 1 in this case.
So, for our case we’ve got to avoid two values of . Namely, since these will give us division by zero. This gives us three possible intervals of validity.
However, only one of these will contain the value of from the initial condition and so we can see that
must be the interval of validity for this solution.
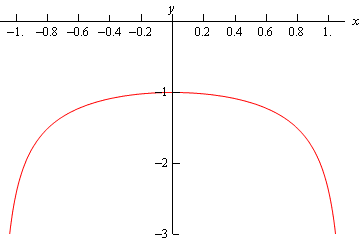
Here is a graph of the solution.
Note that this does not say that either of the other two intervals listed above can’t be the interval of validity for any solution to the differential equation. With the proper initial condition either of these could have been the interval of validity.
We’ll leave it to you to verify the details of the following claims. If we use an initial condition of
we will get exactly the same solution however in this case the interval of validity would be the first one.
Likewise, if we use
as the initial condition we again get exactly the same solution and, in this case, the third interval becomes the interval of validity.
So, simply changing the initial condition a little can give any of the possible intervals.
So, we now have an implicit solution. This solution is easy enough to get an explicit solution, however before getting that it is usually easier to find the value of the constant at this point. So apply the initial condition and find the value of .
Plug this into the general solution and then solve to get an explicit solution.
Now, as far as solutions go we’ve got the solution. We do need to start worrying about intervals of validity however.
Recall that there are two conditions that define an interval of validity. First, it must be a continuous interval with no breaks or holes in it. Second it must contain the value of the independent variable in the initial condition, x = 1 in this case.
So, for our case we’ve got to avoid two values of . Namely, since these will give us division by zero. This gives us three possible intervals of validity.
However, only one of these will contain the value of from the initial condition and so we can see that
must be the interval of validity for this solution.
Here is a graph of the solution.
Note that this does not say that either of the other two intervals listed above can’t be the interval of validity for any solution to the differential equation. With the proper initial condition either of these could have been the interval of validity.
We’ll leave it to you to verify the details of the following claims. If we use an initial condition of
we will get exactly the same solution however in this case the interval of validity would be the first one.
Likewise, if we use
as the initial condition we again get exactly the same solution and, in this case, the third interval becomes the interval of validity.
So, simply changing the initial condition a little can give any of the possible intervals.
Example 2 Solve the following IVP and find the interval of validity for the solution.
This differential equation is clearly separable, so let's put it in the proper form and then integrate both sides.
We now have our implicit solution, so as with the first example let’s apply the initial condition at this point to determine the value of .
The implicit solution is then
We now need to find the explicit solution. This is actually easier than it might look and you already know how to do it. First, we need to rewrite the solution a little
To solve this all we need to recognize is that this is quadratic in and so we can use the quadratic formula to solve it. However, unlike quadratics you are used to, at least some of the “constants” will not actually be constant but will in fact involve ’s.
So, upon using the quadratic formula on this we get.
Next, notice that we can factor a 4 out from under the square root (it will come out as a 2…) and then simplify a little.
We are almost there. Notice that we’ve actually got two solutions here (the “”) and we only want a single solution. In fact, only one of the signs can be correct. So, to figure out which one is correct we can reapply the initial condition to this. Only one of the signs will give the correct value so we can use this to figure out which one of the signs is correct. Plugging = 1 into the solution gives.
In this case it looks like the “+” is the correct sign for our solution. Note that it is completely possible that the “–” could be the solution (i.e. using an initial condition of ) so don’t always expect it to be one or the other.
The explicit solution for our differential equation is.
To finish the example out we need to determine the interval of validity for the solution. If we were to put a large negative value of in the solution we would end up with complex values in our solution and we want to avoid complex numbers in our solutions here. So, we will need to determine which values of will give real solutions. To do this we will need to solve the following inequality.
In other words, we need to make sure that the quantity under the radical stays positive.
Using a computer algebra system like Maple or Mathematica we see that the left side is zero at = –3.36523 as well as two complex values, but we can ignore complex values for interval of validity computations. Finally, a graph of the quantity under the radical is shown below.
So, in order to get real solutions we will need to require because this is the range of ’s for which the quantity is positive. Notice as well that this interval also contains the value of that is in the initial condition as it should.
Therefore, the interval of validity of the solution is .
Here is graph of the solution.
We now have our implicit solution, so as with the first example let’s apply the initial condition at this point to determine the value of .
The implicit solution is then
We now need to find the explicit solution. This is actually easier than it might look and you already know how to do it. First, we need to rewrite the solution a little
To solve this all we need to recognize is that this is quadratic in and so we can use the quadratic formula to solve it. However, unlike quadratics you are used to, at least some of the “constants” will not actually be constant but will in fact involve ’s.
So, upon using the quadratic formula on this we get.
Next, notice that we can factor a 4 out from under the square root (it will come out as a 2…) and then simplify a little.
We are almost there. Notice that we’ve actually got two solutions here (the “”) and we only want a single solution. In fact, only one of the signs can be correct. So, to figure out which one is correct we can reapply the initial condition to this. Only one of the signs will give the correct value so we can use this to figure out which one of the signs is correct. Plugging = 1 into the solution gives.
In this case it looks like the “+” is the correct sign for our solution. Note that it is completely possible that the “–” could be the solution (i.e. using an initial condition of ) so don’t always expect it to be one or the other.
The explicit solution for our differential equation is.
To finish the example out we need to determine the interval of validity for the solution. If we were to put a large negative value of in the solution we would end up with complex values in our solution and we want to avoid complex numbers in our solutions here. So, we will need to determine which values of will give real solutions. To do this we will need to solve the following inequality.
In other words, we need to make sure that the quantity under the radical stays positive.
Using a computer algebra system like Maple or Mathematica we see that the left side is zero at = –3.36523 as well as two complex values, but we can ignore complex values for interval of validity computations. Finally, a graph of the quantity under the radical is shown below.
So, in order to get real solutions we will need to require because this is the range of ’s for which the quantity is positive. Notice as well that this interval also contains the value of that is in the initial condition as it should.
Therefore, the interval of validity of the solution is .
Here is graph of the solution.
Example 3 Solve the following IVP and find the interval of validity of the solution.
First separate and then integrate both sides.
Apply the initial condition to get the value of .
The implicit solution is then,
Now let’s solve for .
Reapplying the initial condition shows us that the “–” is the correct sign. The explicit solution is then,
Let’s get the interval of validity. That’s easier than it might look for this problem. First, since the “inner” root will not be a problem. Therefore, all we need to worry about is division by zero and negatives under the “outer” root. We can take care of both by requiring
Note that we were able to square both sides of the inequality because both sides of the inequality are guaranteed to be positive in this case. Finally solving for we see that the only possible range of ’s that will not give division by zero or square roots of negative numbers will be,
and nicely enough this also contains the initial condition . This interval is therefore our interval of validity.
Here is a graph of the solution.
Apply the initial condition to get the value of .
The implicit solution is then,
Now let’s solve for .
Reapplying the initial condition shows us that the “–” is the correct sign. The explicit solution is then,
Let’s get the interval of validity. That’s easier than it might look for this problem. First, since the “inner” root will not be a problem. Therefore, all we need to worry about is division by zero and negatives under the “outer” root. We can take care of both by requiring
Note that we were able to square both sides of the inequality because both sides of the inequality are guaranteed to be positive in this case. Finally solving for we see that the only possible range of ’s that will not give division by zero or square roots of negative numbers will be,
and nicely enough this also contains the initial condition . This interval is therefore our interval of validity.
Here is a graph of the solution.




Comments
Post a Comment